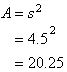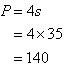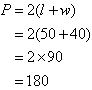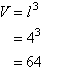Monday, July 11, 2011
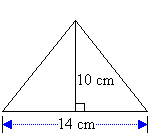
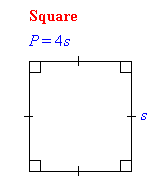
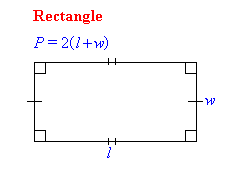
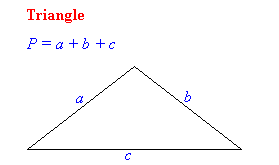
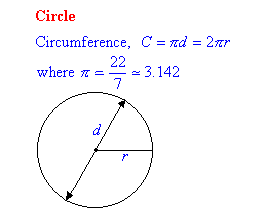
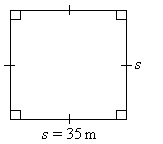
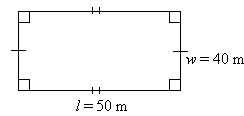
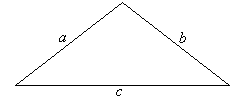
Perimeter
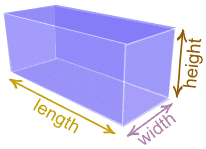
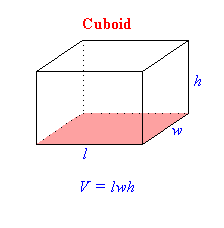
Cuboids, Rectangular Prisms and Cubes
| A cuboid is a box-shaped object. It has six flat sides and all angles are right angles. And all of its faces are rectangles. It is also a prism because it has the same cross-section along a length. In fact it is a rectangular prism. |
|
Examples of Cuboids
Cuboids are very common in our world, from boxes to buildings we see them everywhere. You can even fit them inside other cuboids!
 |  |  |  |
| A box with a slot cut as a handle | Cuboids in a cuboid room | Boxes for model trains | Now that's just silly! |
Volume and Surface Area
The volume of a cuboid is found using the formula:
Volume = Height × Width × Length
Which is usually shortened to:
V = h × w × l
Or more simply:
V = hwl
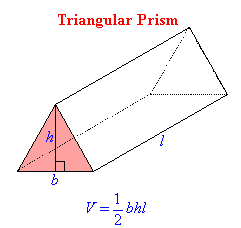
The volume of the following solids are often required to solve real world problems involving quantity, capacity, mass and strength of materials including liquids. | |
|
| |
|
| |
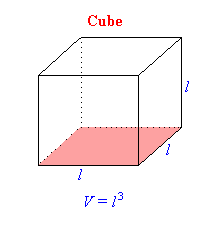
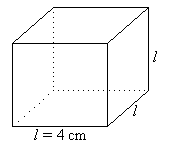
Volume of a CubeExample 25Find the volume of a cube of side 4 cm. | |
|
|
Surface Area
And the surface area is found using the formula:
A = 2wl + 2lh + 2hw
Example: Find the volume and surface area of this cuboid.
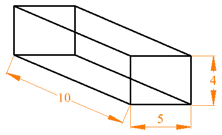 | V = 4×5×10 = 200 A = 2×4×5 + 2×5×10 + 2×10×4 = 40+100+80 = 220 |
Sunday, July 10, 2011
Geometric of Properties
Study the Solids
| In this interactive geometry investigation, students explore geometric solids and their properties. Specifically, students count the number of faces, edges, and corners (vertices) in various solids. |
| | Learning Objectives |
| | Students will:
|

Students should note the following characteristics:
- Each solid has flat sides called faces.
- Each solid has edges to connect the faces.
- Each solid has corners that connect the edges. (Note that the activity sheet refers to corners as "vertices", so you may wish to familiarize students with this vocabulary.)
If you have these shapes in your classroom, have students find the shapes that match those in this computer activity.
This lesson is designed to help students focus on the properties of each shape. The tools allow them to color the faces, edges, or corners (vertices) easily by holding the shift key while clicking the mouse on the paint palette and then on a face. (The edges are always white and the corners black.)Distribute the Exploring Geometric Solids activity sheet to the students.
 | Exploring Geometric Solids Activity Sheet |
Teacher Note: For today's lesson, students will only complete the table on the activity sheet. Save the three questions below the table for tomorrow's lesson.
As students complete the activity sheet, guide them as needed. For example, when asking "How many sides does each face have?", guide the student to click the given face, and color the sides. When determining the number of faces, it may be helpful to color the faces and count as they color. (It's interesting to observe students doing this: some color all faces the same color, while others color the faces different colors.)
After determining the number of faces, students are asked to count the number of edges and vertices (corners) in the solid. Before actually counting the number of edges, students may wish to "guess" the number.
For example, working with the dodecahedron, a student may say each face has five sides — a pentagon. She counts 12 faces. In guessing the number of edges, she may estimate 60 and give as her reason, "5 sides × 12 faces = 60 edges." Counting the edges with the result of 30 provided an opportunity to have her take a second look at the dodecahedron and find out why. (Each edge is shared by two faces.)
Taking advantage of opportunities such as these enriches student understanding.
| | Questions for Students |
| | When you guessed the number of edges in a particular solid, were you correct? Did this affect how you guessed and counted the number of edges in the other solids? [Student responses may vary. Note that students should use their incorrect guesses to inform future predictions.] |
| | Assessment Options |
| |
|
Monday, July 4, 2011
fraction
EXAMPLE:
When you think of a fraction, think of a PIZZA!!
Suppose a pizza is cut evenly into the number of pieces in the DENOMINATOR. If the number of pieces YOU get is the NUMERATOR, the fraction of the pizza you get is:
Adding and taking away (subtracting) fractions can be pictured using slices of pizza. For example:
Multiplying fractions means cutting a portion into smaller portions. For example:
Unit 1 show you how to do this multiplication.
Dividing fractions means determining how many smaller pieces there are in a larger piece. For example:
Add and subtract like fractions
It's easy to add and subtract like fractions, or fractions with the same denominator. You just add or subtract the numerators and keep the same denominator. The tricky part comes when you add or subtract fractions that have different denominators. To do this, you need to know how to find the least common denominator. In an earlier lesson, you learned how to simplify, or reduce, a fraction by finding an equivalent, or equal, fraction where the numerator and denominator have no common factors. To do this, you divided the numerator and denominator by their greatest common factor.
In this lesson, you'll learn that you can also multiply the numerator and denominator by the same factor to make equivalent fractions.
Example 1
![]()
In this example, since 12 divided by 12 equals one, and any number multiplied by 1 equals itself, we know 36/48 and 3/4 are equivalent fractions, or fractions that have the same value. In general, to make an equivalent fraction you can multiply or divide the numerator and denominator of the fraction by any non-zero number.
Since only like fractions can be added or subtracted, we first have to convert unlike fractions to equivalent like fractions. We want to find the smallest, or least, common denominator, because working with smaller numbers makes our calculations easier. The least common denominator, or LCD, of two fractions is the smallest number that can be divided by both denominators. There are two methods for finding the least common denominator of two fractions:
Example 2
![]()
Method 1:
Write the multiples of both denominators until you find a common multiple.
The first method is to simply start writing all the multiples of both denominators, beginning with the numbers themselves. Here's an example of this method. Multiples of 4 are 4, 8, 12, 16, and so forth (because 1 × 4=4, 2 × 4=8, 3 × 4=12, 4 × 4=16, etc.). The multiples of 6 are 6, 12,…--that's the number we're looking for, 12, because it's the first one that appears in both lists of multiples. It's the least common multiple, which we'll use as our least common denominator.
Method 2:
Use prime factorization.
For the second method, we use prime factorization-that is, we write each denominator as a product of its prime factors. The prime factors of 4 are 2 times 2. The prime factors of 6 are 2 times 3. For our least common denominator, we must use every factor that appears in either number. We therefore need the factors 2 and 3, but we must use 2 twice, since it's used twice in the factorization for 4. We get the same answer for our least common denominator, 12.
Example 3
prime factorization of 4 = 2 × 2
prime factorization of 6 = 2 × 3
LCD = 2 × 2 × 3 = 12
Now that we have our least common denominator, we can make equivalent like fractions by multiplying the numerator and denominator of each fraction by the factor(s) needed. We multiply 3/4 by 3/3, since 3 times 4 is 12, and we multiply 1/6 by 2/2, since 2 times 6 is 12. This gives the equivalent like fractions 9/12 and 2/12. Now we can add the numerators, 9 + 2, to find the answer, 11/12.
Example 4
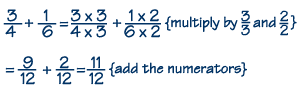
Example 1
Example 2
Example 3
Example 4