Angles
An angle measures the amount of turn
Names of Angles
As the Angle Increases, the Name Changes
| Type of Angle | Description | |
|---|---|---|
| Acute Angle | an angle that is less than 90° | |
| Right Angle | an angle that is 90° exactly | |
| Obtuse Angle | an angle that is greater than 90° but less than 180° | |
| Straight Angle | an angle that is 180° exactly | |
| Reflex Angle | an angle that is greater than 180° |

Be Careful What You Measure
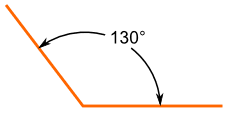 | 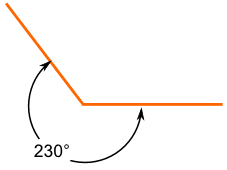 |
| This is an Obtuse Angle. | And this is a Reflex Angle. |
| But the lines are the same ... so when naming the angles make sure | |
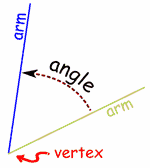 | Parts of an AngleThe corner point of an angle is called the vertex And the two straight sides are called arms The angle is the amount of turn between each arm. |
Labelling Angles
| There are two main ways to label angles: 1. by giving the angle a name, usually a lower-case letter like a or b, or sometimes a Greek letter like α (alpha) or θ (theta) 2. or by the three letters on the shape that define the angle, with the middle letter being where the angle actually is (its vertex). Example angle "a" is "BAC", and angle "θ" is "BCD" | 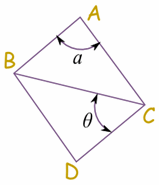 |
Degrees (Angles)
We can measure Angles in Degrees.There are 360 degrees in one Full Rotation (one (Angles can also be measured in Radians) |
(Note: "Degrees" can also mean Temperate, but here we are talking about Angles)
The Degree Symbol: °
We use a little circle ° following the number to mean degrees.
For example 90° means 90 degrees
One Degree
![]()
This is how large 1 Degree is
The Full CircleA Full Circle is 360° Half a circle is 180° Quarter of a circle is 90° | 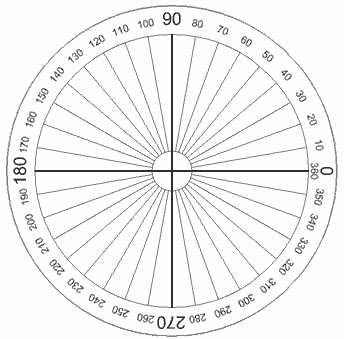 |
| Why 360 degrees? Probably because old calendars (such as the Persian Calendar) used 360 days for a year - when they watched the stars they saw them revolve around the North Star one degree per day. |
Measuring Degrees
We often measure degrees using a protractor: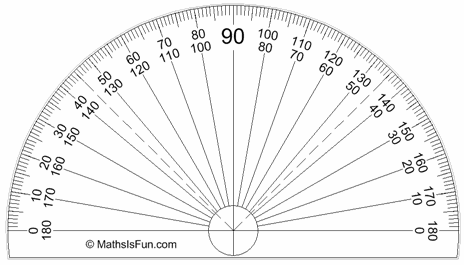
The normal protractor measures 0° to 180°
 | You can also get full-circle protractors. But they are not as commonly used because they are a bit |
Supplementary Angles
These two angles (140° and 40°) are Supplementary Angles, because they add up to 180°. Notice that together they make a straight angle. |  |
But the angles don't have to be together. These two are supplementary because 60° + 120° = 180° |  |
| If the two angles add to 180°, we say they "Supplement" each other. Supplement comes from Latin supplere, to complete or "supply" what is needed. | ||
| Spelling: be careful, it is not "Supplimentary Angle" (with an "i") |
Complementary Angles
Two Angles are Complementary if they add up to 90 degrees (a Right Angle).
These two angles (40° and 50°) are Complementary Angles, because they add up to 90°. Notice that together they make a right angle. | 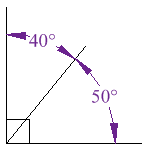 |
But the angles don't have to be together. These two are complementary because 27° + 63° = 90° | 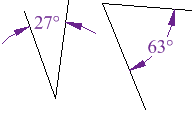 |
Right Angled TriangleIn a right angled triangle, the two acute angles are complementary, because in a triangle the three angles add to 180°, and 90° have been taken by the right angle. |  |
| If the two angles add to 90°, we say they "Complement" each other. Complementary comes from Latin completum meaning "completed" ... because the right angle is thought of as being a complete (full) angle. | ||
| Spelling: be careful, it is not "Complimentary Angle" (with an "i") ... that would be an angle you get for free! |
Complementary vs Supplementary
Note: A related idea is supplementary Angles - those add up to 180°
How can you remember which is which? Easy! Think:
- "C" of Complementary stands for "Corner"
 (a Right Angle), and
(a Right Angle), and - "S" of Supplementary stands for "Straight" (180 degrees is a straight line)
Parallel Lines, and Pairs of Angles
Parallel Lines
Lines are parallel if they are always the same distance apart (called "equidistant"), and will never meet. Just remember:
Always the same distance apart and never touching.
The red line is parallel to the blue line in both these cases:
 |  | |
| Example 1 | | Example 2 |
Parallel lines also point in the same direction.
Pairs of AnglesWhen parallel lines get crossed by another line, you can see that many angles are the same, as in this example: These angles can be made into pairs of angles which have special names.
| 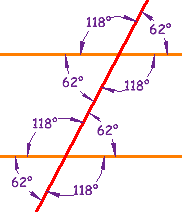 |
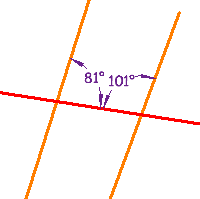
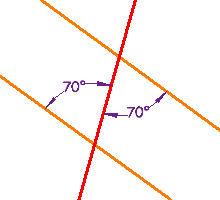
Testing for Parallel Lines
Some of those special pairs of angles can be used to test if lines really are parallel: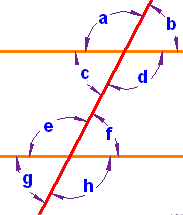 |
|
Examples
Example 2
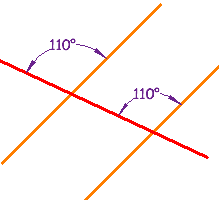

No comments:
Post a Comment