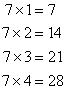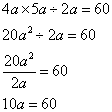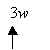| The products of a number with the natural numbers 1, 2, 3, 4, 5, ... are called the multiples of the number. For example:
So, the multiples of 7 are 7, 14, 21, 28, and so on.
|
Monday, June 27, 2011
Multiples
Prime Factor
Example
Find the prime factor decomposition of 36.
We look at 36 and try to find numbers which we can divide it by. We can see that it divides by 2.
36 = 18 × 2
2 is a prime number, but 18 isn't. So we need to split 18 up into prime numbers. We can also divide 18 by 2.
18 = 9 × 2
and so 36 = 18 × 2 = 9 × 2 × 2
But we haven't finished, because 9 is not a prime number. We know that 9 divides by 3.
9 = 3 x 3.
Hence 36 = 9 × 2 × 2 = 3 × 3 × 2 × 2.
This is the answer, because both 2 and 3 are prime numbers.
Example
a and b are prime numbers, ab3 = 54. Find the values of a and b.
So ab3 is the prime factor decomposition of 54.
54 = 2 × 27 = 2 × 3 × 9 = 2 × 3 × 3 × 3 = 2 × 33
So a = 2 and b = 3.
Example 1
Sunday, June 26, 2011
PRIME AND COMPOSITE NUMBERS.
In other words, the prime number can be divided only by 1 and by itself.
NOTE: 0 and 1 are not prime numbers.
Example: 5 is a prime number, because the only factors it has are 1 and 5.
The prime numbers less than 20 are 2,3,5,7,11,13,17,19
Example:
Find all prime factors of 30.
Solution:
All the factors of 30 are 30, 15, 10, 6, 5, 3, 2, 1
But only 5, 3 and 2 are prime numbers.
Thefore all prime factors of 30 are 2, 3 and 5.
A composite number has at least one more factor that the number itself or 1.
In fact, all whole numbers that are not prime are composite except for 1 and 0, which are not prime and not composite.
The composite numbers less than 20 are 4, 6, 8, 9, 10, 12, 14, 15, 16, 18
FACTOR
Example
Write down all factors of 10.
10 = 2 x 5, so numbers 2 and 5 are factors of 10.
Also 10 = 10 x 1, so 10 and 1 are factors of 10.
The factors of 10 are 1, 2, 5, 10.
NOTE: Number 1 and the number itself are always factors of any number.
COMMON FACTORS
Example
Find all the common factors of 12 and 18.
Factors of 12 are 1, 2, 3, 4, 6, 12.Factors of 18 are 1, 2, 3, 6, 18.
The common factors of 12 and 18 are 1, 2, 3 and 6.
COMMON MULTIPLES.
For example, 5 is the first multiple of 5 (because 5 x 1 = 5),
10 is the second multiple of 5, and so on.
Example 1:
Write down the first 3 multiples of 8.
Solution: 8 x 1 = 8, 8 x 2 = 16, 8 x 3 = 24, so the first 3 multiples of 8 are 8,16,24.
Example 2:
Write down all multiples of 3 greater than 10 but smaller than 20.
Solution: Multiples of 3 are 3, 6,9,12,15,18,21,24,...
The desired ones are 12,15,18.
The common multiples of two numbers are multiples of both numbers.
Example 1:
Find common multiples of 3 and 5.
Solution: Multiples of 3 are 3,6,9,12,15,18,21,24,27,30,33,...
Multiples of 5 are 5,10,15,20,25,30,35,...
Common multiples of 3 and 5 are 15, 30, ...
Example 2
LOWEST COMMON MULTIPLE (L.C.M.)
For example, the L.C.M of 3 and 5 is 15 .(see the example above).
The simple method of finding the L.C.M of smaller numbers is to write down the multiples of the larger number until one of them is also a multiple of the smaller number.
Example 1:
Find the Lowest Common Multiple of 8 and 12.
Solution: Multiples of 12 are 12, 24...
24 is also a multiple of 8, so the L.C.M of 8 and 12 is 24.
FINDING L.C.M. OF BIG NUMBERS
- Find all the prime factors of both numbers.
- Multiply all the prime factors of the larger number by those prime factors of the smaller number that are not already included.
Example:
Find the Lowest Common Multiple (L.C.M.) of 240 and 924.
From the example of finding the H.C.F. we know the prime factors of both numbers.
924 = 2 x 2 x 3 x 7 x 11
240 = 2 x 2 x 2 x 2 x 3 x 5
Example 1
Example 2
Example 3
Example 4
Higest Common Factor (HCF)
In other words the H.C.F is the largest of all the common factors.
The common factors or of 12 and 18 are 1, 2, 3 and 6.
The largest common factor is 6, so this is the H.C.F. of 12 and 18.
It is very easy to find a H.C.F. of small numbers, like 6 and 9 (it is 3) or 8 and 4 (it is 4).
The best way is to keep finding the factors of the smaller number, starting from the largest factor. The first factor of the smaller number that is also a factor of the larger number is a H.C.F.
The H.C.F is useful when simplifying fractions.
FINDING THE H.C.F. OF BIG NUMBERS
For larger numbers you can use the following method:
- Find all prime factors of both numbers.
- Write both numbers as a multiplication of prime numbers.
- Find which factors are repeating in both numbers and multiply them to get H.C.F
Example:
Find the Highest Common Factor (H.C.F.) of 240 and 924.
Solution:
Finding all prime factors of 240:
We will start with the smallest prime number and we will divide 240 into it if we can come handy).
We will do the same with the result (or quotient), and we will keep dividing by prime numbers until we have 1 as a quotient.
Each time we write the prime factor to the right and the quotient below:
| 240 | | | 2 | 2 is a factor of 240; | 240 divided by 2 is 120 |
| 120 | | | 2 | 2 is a factor of 120; | 120 divided by 2 is 60 |
| 60 | | | 2 | 2 is a factor of 60; | 60 divided by 2 is 30 |
| 30 | | | 2 | 2 is a factor of 30; | 30 divided by 2 is 15 |
| 15 | | | 3 | 3 is a factor of 15; | 15 divided by 3 is 5 |
| 5 | | | 5 | 5 is a factor of 5; | 5 divided by 5 is 1 |
| 1 |
240 = 2 x 2 x 2 x 2 x 3 x 5
NOTE: There are other methods for finding all prime factors of a number, for example a factor tree.
Finding all prime factors of 924:
| 924 | | | 2 | 2 is a factor of 924; | 924 divided by 2 is 462 |
| 462 | | | 2 | 2 is a factor of 462; | 462 divided by 2 is 231 |
| 231 | | | 3 | 3 is a factor of 231; | 213 divided by 3 is 77 |
| 77 | | | 7 | 7 is a factor of 77; | 77 divided by 7 is 11 |
| 11 | | | 11 | 11 is a factor of 11; | 11 divided by 11 is 1 |
| 1 |
924 = 2 x 2 x 3 x 7 x 11
Multiply the factors which repeat in both numbers to get the H.C.F.
The Highest Common Factor is 2 x 2 x 3 = 12
Example 2
Example 3
Thursday, June 23, 2011
Addition and Substaction
| ADDITION |
| | ||||
| YES - | Same Signs: Find the SUM: | | NO - | Different signs: Find the DIFFERENCE: |
| (-3) + (-6) = (-9) (+4) + (+5) = (+9) | | (+5) + (-7) = (-2) (-4) + (+6) = (+2) | ||
First, change the SUBTRACTION problem to an ADDITION problem;
Then, follow the rules (above) for solving the new ADDITION problem.
(-6) - (+2) =
| First, copy the problem exactly. 1. The first number stays the same. 2. Change the operation. 3. Switch the NEXT SIGN. 4. Follow the rules for addition. | | (-6) - (+2) = (-6) (-6) + (-6) + (-2) (-6) + (-2) = (-8) |
| Subtract means: | (+2) - (-6) = (+2) + (+6) = (+8) | |
| Subtract means: | (-7) - (-3) = (-7) + (+3) = (-4) | |
| Subtract means: | (+4) - (+9) = (+4) + (-9) = (-5) |
First, DO the multiplication or division.
Then determine the sign:
Count the number of negative signs....
| YES | (an EVEN number of negative signs) | the answer is POSITIVE |
| NO | (an ODD number of negative signs) | the answer is NEGATIVE |
| First, copy the problem exactly. | | (-2) * (-4) * (-6) = |
| DO the multiplication or division. | | |2| * |4| * |6| = |48| |
| Count the number of negative signs.... | | (-2) * (-4) * (-6) = |
Are there an EVEN number of negatives? | | A total of THREE NEGATIVES Three is NOT EVEN (it's odd). So the answer is NEGATIVE -48 |
| A total of ZERO NEGATIVES Zero IS EVEN . So the answer is POSITIVE | | A total of ONE NEGATIVE One is NOT EVEN (it's odd). So the answer is NEGATIVE | | A total of TWO NEGATIVES TWO IS EVEN . So the answer is POSITIVE |
Sunday, June 19, 2011
Cara Mendapatkan Fail Flash (multimedia) Daripada Laman Learning Management System KPM
1. Anda perlu mendaftar di laman LMS Kementerian Pelajaran Malaysia.


2. Lengkapkan butiran dan maklumat untuk aktivate akan dihantar ke email anda.
3. Pilih subjek yang dikehendaki. Contoh berikut:

4. Pop up windows akan keluar. Tunggu sehingga semua fail di muat turun ke dalam komputer anda. Ikut langkah demi langkah sehingga penghujung. Fail-fail tersebut akan kekal dalam folder sementara.
5. Klik Tools dan pilih internet options. Klik setting.

6. klik kat view files.

7. Tulis swf dalam kotak search. Klik size untuk melihat fail yang besar dan jangan lupa rujuk juga tarikh dan masa anda menggunakannya.

8. Salin fail tersebut ke folder anda. Anda perlukan perisian GOM Player atau IE untuk melarikan fail swf.

9. Ini contohnya.
Selamat mencuba kepada pelajar OUM.
Friday, June 17, 2011
Algebraic Expression - How to simplify problems
Combine Like Terms
Like terms are terms that have the same variable part i.e. they only differ in their coefficients. Combining like terms is very often required in the process of simplifying equations.
For example:
2x and –5x are like terms
a and
are like terms
6x and 5y are unlike terms
Like terms can be added or subtracted from one another.
For example:
a + a = 2 × a = 2a (We usually write 2 × a as 2a)
2a + 4a = 6a
a + a + a = 3a
2a + 4 (Unlike terms cannot be simplified)
4a + 3b (Unlike terms cannot be simplified)
6a – 3a = 3a
8b – 8b = 0
5a – 3 (Unlike terms cannot be simplified)
6a – 4b (Unlike terms cannot be simplified)
Example 1:
Simplify: 8xy – 5yx = 1
Solution:
Step 1: 5yx is the same as 5xy using the
commutative propertyStep 2: Since the right side is already simple, we can work on the left side expression:
8xy – 5yx = 8xy – 5xy = 3xy
Putting back the left side and right side of the equation:
3xy = 1
Answer: 3xy = 1
Example 2:
Simplify: 7a + 5b – 6b + 8a + 2b = 0
Solution:
Step 1: Group together the like terms:
7a + 5b – 6b + 8a + 2b = 0
(7a + 8a) + (5b – 6b + 2b) = 0
Step 2: Then simplify:
15a + b = 0
Answer: 15a + b = 0
Multiplication and Division of Terms
The coefficients and variables of terms can be multiplied or divided together in the process of simplifying equations.
For example:
3 × 4b = 3 × 4 × b = 12b
5a × 3a = 5 × a × 3 × a = 5 × 3 × a × a = 15a2 (using exponents)
| Beware! | a × a = a2 |
| a + a = 2a |
Example 1:
Simplify: 4a × 5a ÷ 2a = 60
Solution:
Step 1: Perform the multiplication and division
Step 2: Isolate variable a
Answer: a = 6
Removal of Brackets - Distributive Property
Sometimes removing brackets (parenthesis) allows us to simplify the expression. Brackets can be removed by using the distributive property. This is often useful in simplifying equations.
For example:
3(a – 3) + 4 = 3 × a + 3 × (-3) + 4 = 3a – 9 + 4 = 3a – 5
5 – 6 (b + 1) = 5 + ( – 6 ) × b + (– 6) × 1 = 5 – 6b – 6 = – 6b – 1
Example 1:
Simplify: 5(a – 4) + 3 = 8
Solution:
Step 1: Remove the brackets
5a – 20 + 3 = 8
Step 2: Isolate variable a
5a = 8 – 3 + 20
5a = 25
Answer: a = 5
Cross Multiplication
Cross multiplication allows you to remove denominators from fractions in an equation. Note that this technique applies only towards simplifying equations, not to simplifying expressions.
For example, if you have the equation:
then you can multiply the numerator of one fraction with the denominator of the other fraction (across the = sign) as shown:
to obtain the equation
(2 × 6) = a × 3
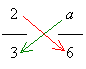
Example 1:
Simplify: ![]()
Solution:
Step 1: Cross Multiply
4 × a = 8 × 5
4a = 40
Step 2: Isolate variable a
Answer: a = 10
In the equation 3x – 2 = 16, notice that the variable is being multiplied and has a term being subtracted. To isolate the variable, we need to add 2 to both sides and then divide both sides by 3.
Example:
Solve 3x – 2 = 16
Solution:
3x – 2 = 16
3x – 2 + 2 = 16 + 2 (add 2 to both sides)
3x = 18 (simplify)
x = 6 (divide both sides by 3)
Check:
3x – 2 = 16
3 • 6 – 2 = 16 (Substitute x = 6 into the original equation)
Consider the equation,
Example:
Solve ![]()
Solution:
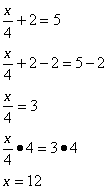
Check:
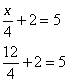
Solving multi-step equations with whole numbers
To solve a multi-step equation, we would start by trying to simplify the equation by combining like terms and using the distributive property whenever possible.
Consider the equation 2(x + 1) – x = 5. First, we will use the distributive property to remove the parenthesis and then we can combine like terms and the isolate the variable.
Example:
Solve 2(x + 1) – x = 5
Solution:
2(x + 1) – x = 5
2x + 2 – x = 5 (use distributive property)
x + 2 = 5 (combine like terms)
x + 2 – 2 = 5 – 2
x = 3
Solving Multi-Step Equations With Fractions
To solve an equation with fractions, we first try to change it into an equation without fractions. Then, we can solve it using the methods we already know.
Consider the equation ![]() . To remove the fractions, we would need to multiply each term of the equation with the LCM of the denominator. In this case, we will multiply each term with 4. The 4 will cancel and we are left with equation 2x – 12 = 3. To isolate the variable, we will add 12 to both sides and then divide by 2.
. To remove the fractions, we would need to multiply each term of the equation with the LCM of the denominator. In this case, we will multiply each term with 4. The 4 will cancel and we are left with equation 2x – 12 = 3. To isolate the variable, we will add 12 to both sides and then divide by 2.
Example:
Solve ![]()
Solution:
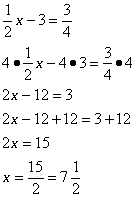
Wednesday, June 15, 2011
Algebraic Expression - simplify
To simplify an algebraic expression that consists of both like and unlike terms, it might be helpful to first move the like terms together. (When moving the terms, we must remember to move the + or – attached in front of them).
For example,
3x + 2y – 2x + 6
= 3x– 2x + 2y + 6
= (3 – 2)x + 2y + 6
= x + 2y + 6
Example:
Simplify 3x + 2a – 4x
Solution:
3x + 2a – 4x
=3x– 4x + 2a
= (3 – 4)x + 2a
= –x + 2a
Example 1
Example 2:
Example 3
Algebraic Expression - unlike and like
Like terms are terms that have the same variable part i.e. they only differ in their coefficients.
For example:
2x and –5x are like terms
a and
are like terms
6x and 5y are unlike terms
Like terms can be added or subtracted from one another.
Example :
Simplify the expressions:
a) 14x + 5x
b) 5y – 13y
c) p – 3p
Solution:
a) 14x + 5x = (14 + 5)x = 19x
b) 5y – 13y = (5 –13)y = –8y
c) p – 3p = (1 – 3)p = – 2p
Algebraic Expression - Coefficient
Coefficients
The coefficient of a variable is the number that is placed in front of a variable.
For example, 3 × w can be written as 3w and 3 is the coefficient.
CoefficientCoefficients Of Algebraic Terms
The number (positive or negative) in the algebraic term is called the coefficient.
For example:
For the term 4x, 4 is the coefficient
For the term –7y, –7 is the coefficient
The coefficient of 1 in an algebraic term is usually not written.
For example:
1y can be written as simply y. So, 1y and y are the same.
Example:
Find the coefficient and variable of each of the following terms:
a) 0.2m
b) –3p
c)
q
d) z
e)
Solution:
a) 0.2m (The coefficient is 0.2 and the variable is m)
b) –3p (The coefficient is –3 and the variable is p)
c)
q (The coefficient is
and the variable is q)
d) z (The coefficient is 1 and the variable is z)
e)
(The coefficient is
and the variable is x)
Algebraic Expression - Term
Terms
A term can be any of the following:
- a constant: e.g. 3, 10, π,
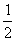
- the product of a number (coefficient) and a variable: e.g. –3x, 11y,
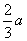
- the product of two or more variables: e.g. x2, xy, 2y2, 7xy
Like terms are terms that differ only in their numerical coefficients. For example: 3a, 22a, ![]() are like terms.
are like terms.
Expressions
An expression is made up of one or more terms.
For example:
3w + 4xy + 5
An expression can be term or a collection of terms separated by addition or subtraction operators. Some examples of expressions, with the numbers of terms, are listed below:
Expression | Number of Terms | Description |
6x | 1 | A number multiplied by a variable. The number is always written first followed by the variable(s). |
3w – 8 | 2 | Terms separated by – |
7b + 5t – 6 | 3 | Terms separated by + and – |
| 1 | All multiplication and division, no + or – symbol |
Example:
Determine the number of terms in the following expressions:
a) 5xyz
b) 3x + 2y – 2x + 6
Solution:
a) 5xyz has one term
b) 3x + 2y – 2x + 6 has four terms
Algebraic Expression
In mathematics, often the value of a certain number may be unknown. A variable is a symbol, usually a letter, which is used to represent an unknown number.
Some examples of variables are:
x, a, t, y, b
A term can be a number, a variable, or a number and variable combined by multiplication or division.
Some examples of terms are:
x, 8, 4y,
Monday, June 13, 2011
Solid Geometry
Solid geometry is concerned with three-dimensional shapes. Some examples of three-dimensional shapes are cubes, rectangular solids, prisms, cylinders, spheres, cones and pyramids. We will also discuss some nets of solids.
Cubes
A cube is a three-dimensional figure with six matching square sides.
The figure above shows a cube. The dotted lines indicate edges hidden from your view.
If s is the length of one of its sides, the
Volume of the cube = s3
Since the cube has six square-shape sides, the
Surface area of a cube = 6s2Rectangular Solids
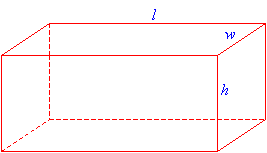
In a rectangular solid, the length, width and height may be of different lengths.
The volume of the above rectangular solid would be the product of the length, width and height that is
Volume of rectangular solid = lwh
Surface area of rectangular solid = 2(lw + wh + lh)
Quiz sectionPlease answer question here.