Combine Like Terms
Like terms are terms that have the same variable part i.e. they only differ in their coefficients. Combining like terms is very often required in the process of simplifying equations.
For example:
2x and –5x are like terms
a and
are like terms
6x and 5y are unlike terms
Like terms can be added or subtracted from one another.
For example:
a + a = 2 × a = 2a (We usually write 2 × a as 2a)
2a + 4a = 6a
a + a + a = 3a
2a + 4 (Unlike terms cannot be simplified)
4a + 3b (Unlike terms cannot be simplified)
6a – 3a = 3a
8b – 8b = 0
5a – 3 (Unlike terms cannot be simplified)
6a – 4b (Unlike terms cannot be simplified)
Example 1:
Simplify: 8xy – 5yx = 1
Solution:
Step 1: 5yx is the same as 5xy using the
commutative propertyStep 2: Since the right side is already simple, we can work on the left side expression:
8xy – 5yx = 8xy – 5xy = 3xy
Putting back the left side and right side of the equation:
3xy = 1
Answer: 3xy = 1
Example 2:
Simplify: 7a + 5b – 6b + 8a + 2b = 0
Solution:
Step 1: Group together the like terms:
7a + 5b – 6b + 8a + 2b = 0
(7a + 8a) + (5b – 6b + 2b) = 0
Step 2: Then simplify:
15a + b = 0
Answer: 15a + b = 0
Multiplication and Division of Terms
The coefficients and variables of terms can be multiplied or divided together in the process of simplifying equations.
For example:
3 × 4b = 3 × 4 × b = 12b
5a × 3a = 5 × a × 3 × a = 5 × 3 × a × a = 15a2 (using exponents)
| Beware! | a × a = a2 |
| a + a = 2a |
Example 1:
Simplify: 4a × 5a ÷ 2a = 60
Solution:
Step 1: Perform the multiplication and division
Step 2: Isolate variable a
Answer: a = 6
Removal of Brackets - Distributive Property
Sometimes removing brackets (parenthesis) allows us to simplify the expression. Brackets can be removed by using the distributive property. This is often useful in simplifying equations.
For example:
3(a – 3) + 4 = 3 × a + 3 × (-3) + 4 = 3a – 9 + 4 = 3a – 5
5 – 6 (b + 1) = 5 + ( – 6 ) × b + (– 6) × 1 = 5 – 6b – 6 = – 6b – 1
Example 1:
Simplify: 5(a – 4) + 3 = 8
Solution:
Step 1: Remove the brackets
5a – 20 + 3 = 8
Step 2: Isolate variable a
5a = 8 – 3 + 20
5a = 25
Answer: a = 5
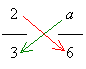
Cross Multiplication
Cross multiplication allows you to remove denominators from fractions in an equation. Note that this technique applies only towards simplifying equations, not to simplifying expressions.
For example, if you have the equation:
then you can multiply the numerator of one fraction with the denominator of the other fraction (across the = sign) as shown:
to obtain the equation
(2 × 6) = a × 3
Example 1:
Simplify: ![]()
Solution:
Step 1: Cross Multiply
4 × a = 8 × 5
4a = 40
Step 2: Isolate variable a
Answer: a = 10
In the equation 3x – 2 = 16, notice that the variable is being multiplied and has a term being subtracted. To isolate the variable, we need to add 2 to both sides and then divide both sides by 3.
Example:
Solve 3x – 2 = 16
Solution:
3x – 2 = 16
3x – 2 + 2 = 16 + 2 (add 2 to both sides)
3x = 18 (simplify)
x = 6 (divide both sides by 3)
Check:
3x – 2 = 16
3 • 6 – 2 = 16 (Substitute x = 6 into the original equation)
Consider the equation,
Example:
Solve ![]()
Solution:
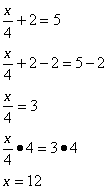
Check:
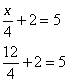
Solving multi-step equations with whole numbers
To solve a multi-step equation, we would start by trying to simplify the equation by combining like terms and using the distributive property whenever possible.
Consider the equation 2(x + 1) – x = 5. First, we will use the distributive property to remove the parenthesis and then we can combine like terms and the isolate the variable.
Example:
Solve 2(x + 1) – x = 5
Solution:
2(x + 1) – x = 5
2x + 2 – x = 5 (use distributive property)
x + 2 = 5 (combine like terms)
x + 2 – 2 = 5 – 2
x = 3
Solving Multi-Step Equations With Fractions
To solve an equation with fractions, we first try to change it into an equation without fractions. Then, we can solve it using the methods we already know.
Consider the equation ![]() . To remove the fractions, we would need to multiply each term of the equation with the LCM of the denominator. In this case, we will multiply each term with 4. The 4 will cancel and we are left with equation 2x – 12 = 3. To isolate the variable, we will add 12 to both sides and then divide by 2.
. To remove the fractions, we would need to multiply each term of the equation with the LCM of the denominator. In this case, we will multiply each term with 4. The 4 will cancel and we are left with equation 2x – 12 = 3. To isolate the variable, we will add 12 to both sides and then divide by 2.
Example:
Solve ![]()
Solution:
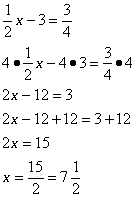
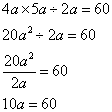

No comments:
Post a Comment